Region-aided Geometric Snake

An enhanced, region-aided, geometric active contour that is more tolerant towards weak edges and noise in images is introduced. The proposed method integrates gradient flow forces with region constraints, composed of the image region vector flow forces obtained through the diffusion of the region segmentation map. We refer to this as the Region-aided Geometric Snake or RAGS. The diffused region forces can be generated from any reliable region segmentation technique, greylevel or colour. This extra region force gives the snake a global view of the boundary information within the image which, along with the local gradient flow, helps detect fuzzy boundaries and overcome noisy regions. The partial differential equation (PDE) resulting from this integration of image gradient flow and diffused region flow is implemented using the level set approach. We present various examples and also evaluate and compare the performance of RAGS on weak boundaries and noisy images.

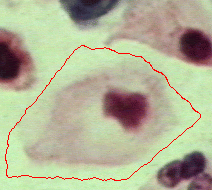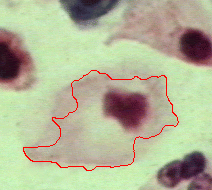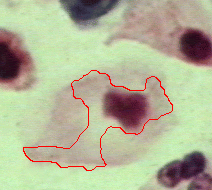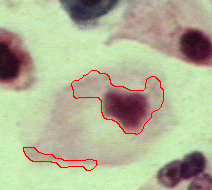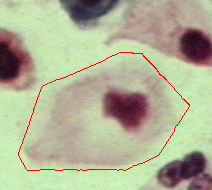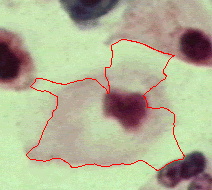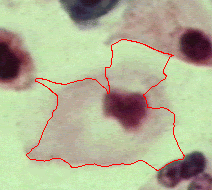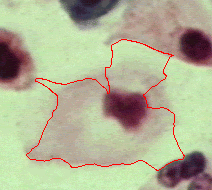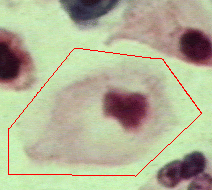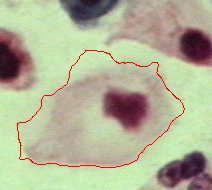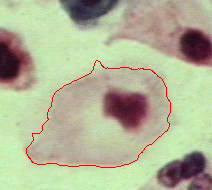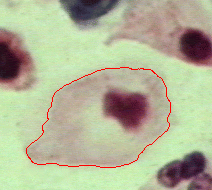Geodesic snakeGeneralised GVFProposed RAGS model

Geodesic Snake (Standard Geometric Snake)

Geometric models of active contours were simultaneously proposed by Caselles et al. and by Malladi et al. in 1993. Geometric snakes are represented implicitly and evolve according to an Eulerian formulation. They are based on the theory of curve evolution implemented via level set algorithms and automatically handle changes in topology when numerically implemented using level sets. Hence, without resorting to dedicated contour tracking, unknown numbers of multiple objects can be detected simultaneously. Furhthermore, geometric snakes can have much larger capture areas than parametric snakes.

Using a reaction-diffusion model from mathematical physics a planar contour is evolved with a velocity in the direction normal to the curve. The velocity contains two terms: a constant motion term that leads to the formation of shocks from which a representation of shape can be derived, and a curvature term that smooths the front, showing up significant features and shortening the curve.

Here is an example on colour image (this image is taken from "Color Snake" by G. Sapiro in 1997):

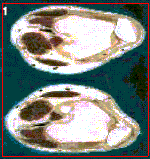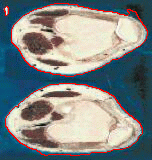Initial SnakeConverged Geodesic Snake

Level Set Method

Level set method is a computational technique for tracking a propagating interface over time. This method has been used in a variety of aspects of image processing. The merging and splitting of evolving curves can be easily handled by implementing this method.

In this approach, the snake is embedded as a zero level set of a three-dimensional surface.

The following example shows how the level set method works.

SnakeLevel Set

Motion Under Curvature Flow

The curvature for a two-dimensional curve given implicitly by g(x, y)=0 is given by

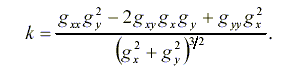The curvature measure how fast a curve moves at any point. While evolving under curvature flow, each point on the curve moves perpendicular to the curve, parallel to its normal direction, with speed proportional to its curvature. The curvature could be written as

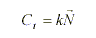The level set representation is given by

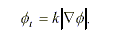It has a well-known attribute. A simple closed curve, no matter how twisted it is, will evolve toward a circular shape and will disappear under the curvature flow (see the next moive).

Initial CurveEvolving CurveMovie

Motion Under Constant Flow

The constant motion could be written as

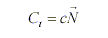where c is a constant. Its level set representation could be written as

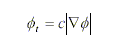A smooth embedded curve shrinking under curvature flow remains regular; that is the flow is indeed smoothing. The constant flow on the other hand can cause a smooth curve to evolve to a singular one. This is also one of the desirable characteristics since the resulting shocks are important features for the object detection.

Initial CurveEvolving CurveMovie

Geodesic Snake

The formulation of the geodesic snake is given by

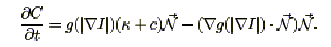and its level set representation is

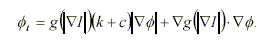Here we present another example on a gray-level image.

Initial SnakeConverged Geodesic SnakeMovie

Problems

The constant flow term makes the snake expand or shrink. It can speed up the convergence and push the snake to concavities easily when the objects have good contrast, i.e. the gradient values at object boundaries are large. However, when the object boundary is indistinct or has gaps, the snake tends to leak through the boundary because of the constant force. The second term in geodesic snake formulation is designed to attract the contour closer to the object boundary, also to pull back the contour if it leaks through the boundary. But the force is not strong enough, because it still depends on the gradient values. It does not solve the weak-edge leakage problem.

Here is an example on a synthetic image.

Region-aided Geometric Snake

Here we propose a novel approach to make the geometric snake much more tolerant towards weak-edges. It comprises the integration of the gradient flow forces with diffused region forces in the image resulting in the Region-aided Geometric Snake.

The gradient flow force supplants the snake with local object boundary information. The region force is based on the global features in the image. When reaching the vicinity of the region boundary, the proposed snake tries to rest on the local maximum based on the gradient flow forces. The steady state of the snake is the equilibrium state of the gradient forces and region force.

The region-aided geometric snake formulation is given by

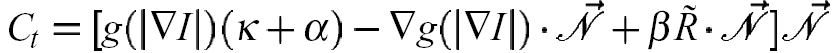where R is the region force vector field, which is obtained from the region segmentation. The term alpha and beta are constants, a trade-off between gradient forces and region forces. The RAGS evolves under all the internal and external forces. Its level set representation is

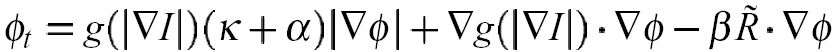Experimental Results

In the following section, we will domenstrate that the region-aided geometric snake can be much more robust toward weak-edges in images, and more tolerable to noise. The diffused region constriants can be generated in a vaiety of ways, and acts as an extra image constraint. We will show a good degree of tolerance to segmentation quality, and our snake can indeed also act as a refinement of the results of the earlier region segmentation.

Preventing Weak-edge Leakage

  • The first example is tested on a synthetic image:

Top row: geodesic snake steps through; Bottom row: region-aided geometric snake rests using extra region constraint.

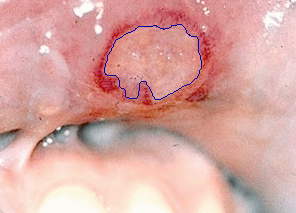
  • The next example is tested on a colour medical image:
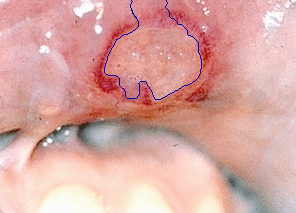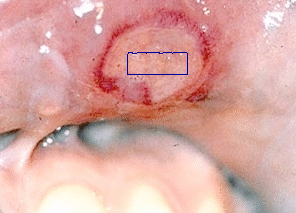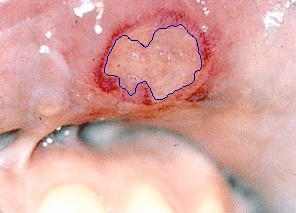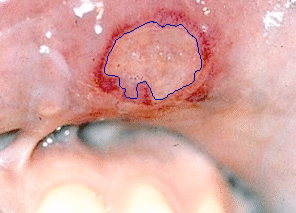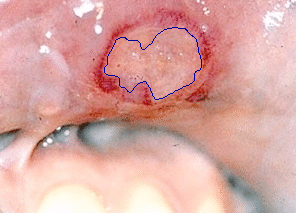Geodesic snake segmentation resultRegion-aided snake segmentation result
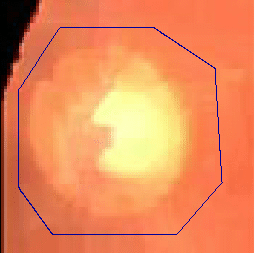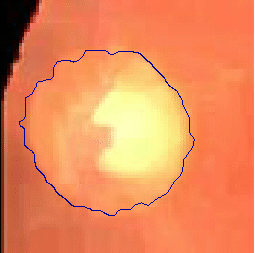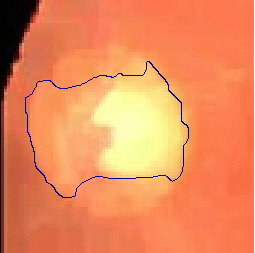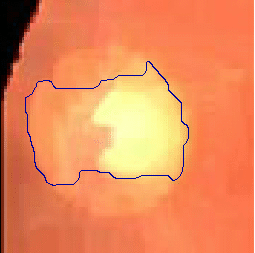
  • The following two examples are tested on close-up retinal images after morphological pre-processing
Geodesic snake segmentation resultRegion-aided snake segmentation result
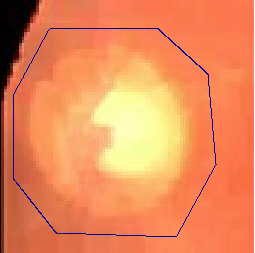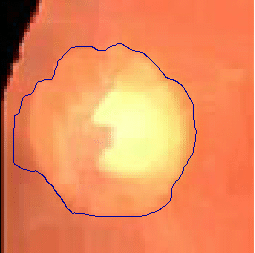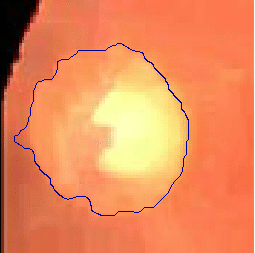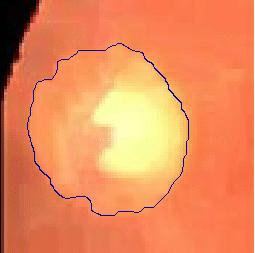Geodesic snake segmentation resultRegion-aided snake segmentation result
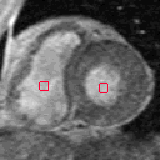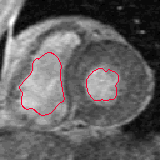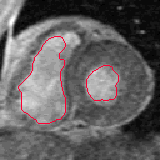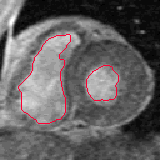
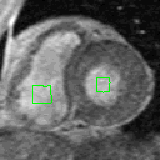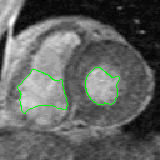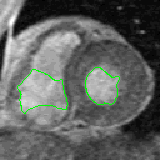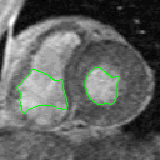
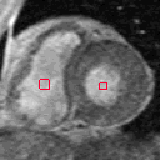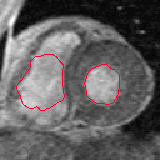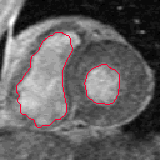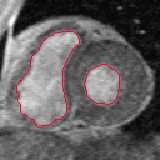
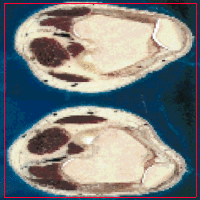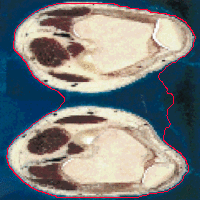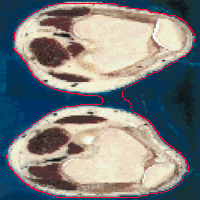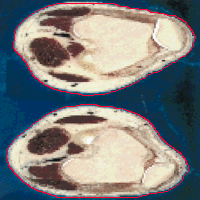
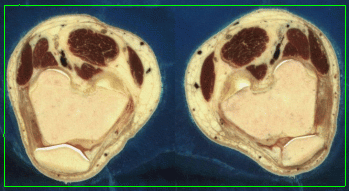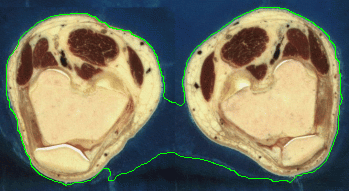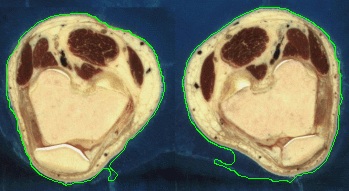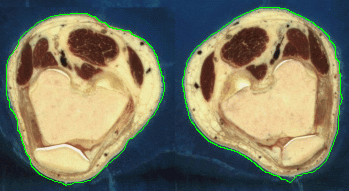
  • The next example shown is testing on an MRI image.
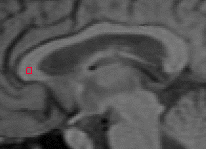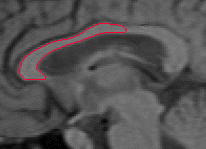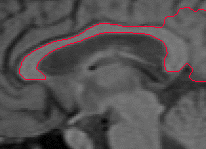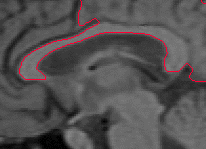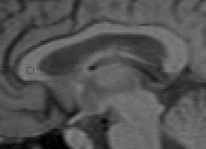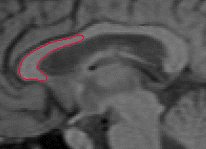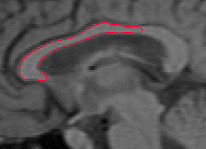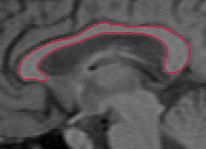Geodesic snake segmentation resultRAGS segmentation result

Testing on Noisy Images

We show that this combination of forces not only improves the performance of the geometric snake toward weak edges, but also makes it more immune to noise.

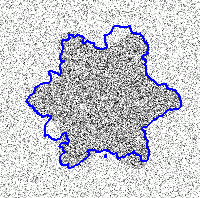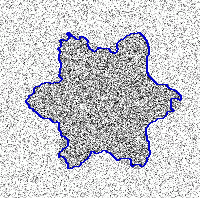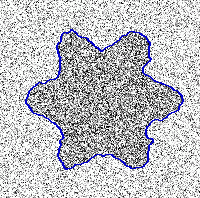Original image with imposed noise from 10% to 60%GGVF snake segmentation resultsGeodesic snake segmentation resultsRAGS segmentation results

The quantitative MRE results are shown in the following table:

% noiseStandard Geometric Snake ErrorGGVF Snake ErrorRAGS Snake Error
02.002.002.00
102.232.242.00
205.007.074.03
3010.0016.033.41
4016.6121.315.22
5015.8121.005.38
6028.1720.105.83

Different Region-force Generation

The region force can be generated from any image segmentation technique, e.g. colour segmentation such as mean shift algorithm by D. Comaniciu and P. Meer, and acts as an extra image constraint. This means that while our proposed method is independent of any particular segmentation technique, it is dependent on the quality of the regions produced. However, we show a good degree of tolerance to segmentation quality, and that our snake can indeed also act as a refinement of the results of the earlier region segmentation.

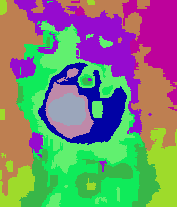
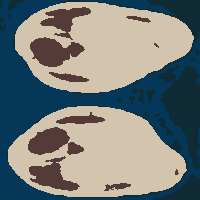
In the following examples, under-segmentation and over-segmentation are implemented to split the image into regions.

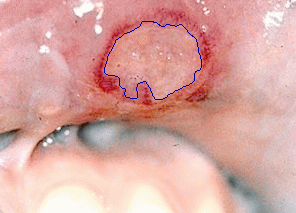Mean shift under-segmentationRegion-aided snake segmentation result
Mean shift over-segmentationRegion-aided snake segmentation result
Mean shift under-segmentationRegion-aided snake segmentation result
Mean shift over-segmentationRegion-aided snake segmentation result
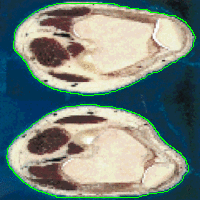Mean shift under-segmentationRegion-aided snake segmentation result
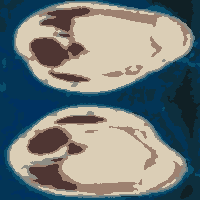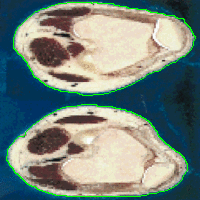Mean shift over-segmentationRegion-aided snake segmentation result

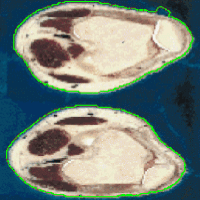
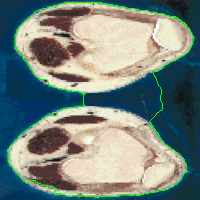
More Testing Results

  • Segmentation accuracy comparison
Geodesic snake segmentationGGVF snake segmentationRAGS segmentation result
Geodesic snake segmentationGGVF snake segmentationRAGS segmentation result
Geodesic snake segmentationGGVF snake segmentationRAGS segmentation result
Geodesic snake segmentationGGVF snake segmentationRAGS segmentation result
  • Further results
RAGS segmentation resultRAGS segmentation resultRAGS segmentation result

The first image shows the region-aided snake segmentation on a retinal colour image with blood vessels removement pre-processing; the second one shows the proposed snake working on a retinal image with blood vessels, the snake splits into two curves to localise the optic disk.

Publications