MAC-Magnetostatic Active Contour Model
We propose an active contour model using an external force field that is based on magnetostatics and hypothesised magnetic interactions between the active contour and object boundaries. The major contribution of the method is that the interaction of its forces can greatly improve the active contour in capturing complex geometries and dealing with difficult initializations, weak edges and broken boundaries. The proposed method is shown to achieve significant improvements when compared against six well-known and state-of-the-art shape recovery methods, including the geodesic snake, the generalised version of GVF snake, the combined geodesic and GVF snake, and the charged particle model.
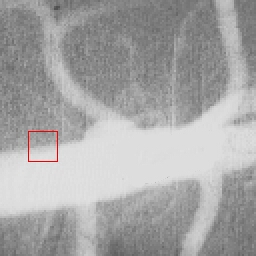 | 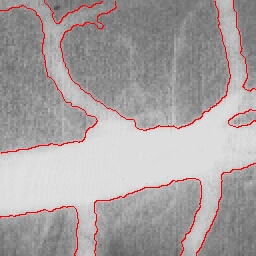 | 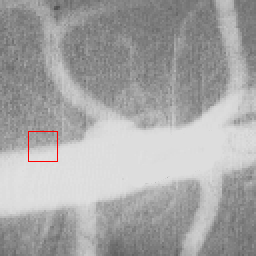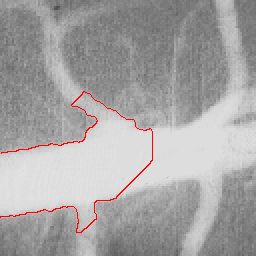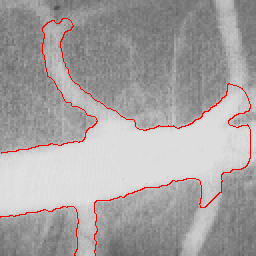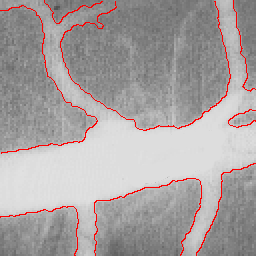 |
| Initial MAC Snake | Converged MAC Snake | MAC Evolution |
Proposed Method
Our approach is to define a novel, single, external bidirectional force field which has the ability to dynamically update itself while the contour evolves. This is significantly different from other works and we emphasise that it does not involve the introduction of any extra forces to mobilise the force field.
In brief, we hypothesise electric currents flowing through both the object boundary and the active contour. The magnetic fields generated by each of the currents will interact and cause a force between them. This magnetic vector force field behaves as an external force to push or pull the active contour towards the object boundary. Although the magnetic field caused by the image gradient is stationary, the force it imposes on the snake is dependent on the snake’s evolution. Thus the force field is dynamically changing along with the snake. We show that by using this electromagnetic interaction analogy between image gradients and active contours, the snake is then much less sensitive to its initial position and much more robust towards complex geometries and topologies.
Next, we present the basic theory of magnetostatics which is used to provide the analogy for our magnetostatic active contour (MAC). The Level Set method is then used to implicitly represent and evolve MAC.
The magnetostatic field
Consider two points P and Q with charges, qP and qQ, and velocity vectors uP and uQ, respectively (see the figure below). These charged wires exert magnetic forces unpon each other. The figure below illustrates the magnetic field exerted due to C2. The red crosse symbols denote the magnetic field going perpendicularly into the image plane, and those blue dot symbols denote the magnetic field that are coming out of the image plane. It can be calculated by integrating the magnetic field produced by infinitesimal current segment on C2.
This magnetic field then generates a force on C1. The point P on C1 will be enforced an expansion force as indicated by the red arrow in the figure. This relationship can be quantified using the Biot-Savart law.
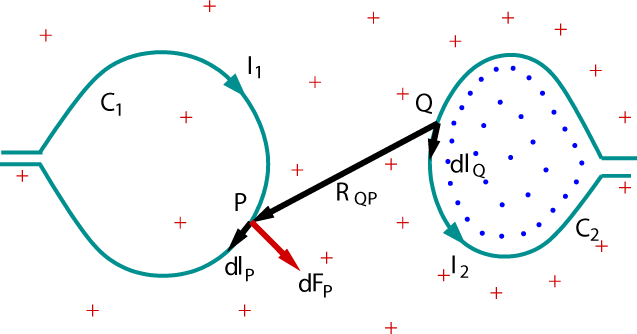 |
The MAC model
Magnetostatic theory is applied to our active contour model by charging both the object boundary and the active contour with electric currents. The concept is represented again in previous figure by treating C1 as an active contour and C2 as an object boundary. As we are interested in the deformation of the contours, only the forces exerted by the object boundary on the active contour are needed. In other words, we shall ignore magnetic forces introduced by the active contour. We then obtain an estimation of the hypothesised direction of the currents in the object boundary and the active contour, and compute the resulting magnetic flux density at each pixel position in the image.
Briefly, it involves the following steps:
- Object boundary orientation estimation;
- Snake current direction estimation;
- Magnetic field computation;
- Force extension and Level Set based snake evolution.
The MAC model is formulated as:
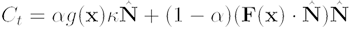 , , |
where F denotes the magnetic force computed as an interaction between object boundary and active contours.
MAC has the distinctive feature in that its direction relies on both spatial position and the evolving contour. The external bidirectional force is dynamically adaptive based on contour position, and equally importantly its direction is always normal to the evolving contour. The strength is determined by the magnitude of the magnetic field, thus the snake can be initialised across the object boundary and reach into concavities. We will demonstrate this later by comparing with six other deformable models.
Edge perserving magnetic force field diffusion
In keeping with other snake models based on image gradients, MAC can also suffer from image noise. Here, we perform diffusion based on the idea for the GVF/GGVF snakes to refine the magnetic force field when necessary. However, we modify the diffusion functions in order to better preserve edges and show that in our case only diffusing a scalar field, rather than a vector field, is sufficient. Thus, there is also a gain in computational efficiency.
Here is an example of refining the magnetic field when necessary:
 |  |  |
| Noise corrupted image | Initial magnetic field (magnitude) | Refined magnetic field (magnitude) |
Implementation
The main computational costs lay in two stages: evolving the level set function and computing the magnetic flux density. The Narrow Band approach is used in order to save on costs associated with updating the level set function. The summation involved in the magnetic flux density computation is generally computationally expensive. However, this can be significantly reduced by letting only edge pixels be involved in the summation. More savings can be made by approximating the flux density based on interactions in a fixed radial distance Rc, instead of across the whole image. Rc should be reasonably large to prevent null flux density.
Alternatively, a slightly less precise but an even faster approach can be used based on the relationship between the magnetic field and the magnetic vector potential. By separating the two orthogonal components of the magnetic vector potential, we can efficiently and sufficiently estimate each of them using the PPPM method or the FFT-based method.
Experimental Results
To objectively examine MAC’s initialization invariancy and convergence ability, we first present results on various shape geometries and topologies using synthetic images with welldefined object boundaries. These include the four-disc problem, acute concavities, multiple objects with complex geometry and topology, and imperfect boundaries.
We then present comparative study on real images. The MAC model is compared against six well-known and state-of-the-art deformable models: the distance vector flow (DVF) snake, the geodesic snake, the generalised version of GVF (GGVF) snake, the geodesic GVF/GGVF (GeoGVF/GeoGGVF) snake, the curvature vector flow (CVF) snake, and the charged particle model (CPM).
1. The four-disc problem
- Outside boundary initialisation
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF |  | 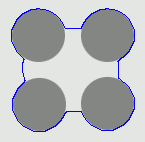 |  |
| Geodesic |  |  |  |
| GGVF |  | 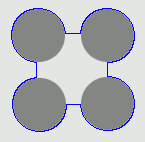 |  |
| GeoGGVF |  | 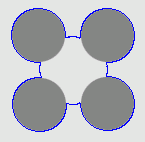 |  |
| CVF |  | 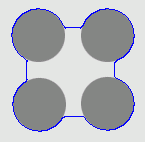 |  |
| MAC |  |  |  |
- Cross boundary initialisation
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF | 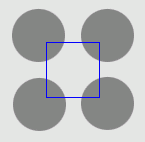 | 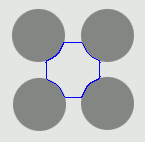 | 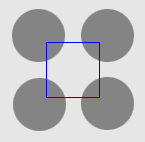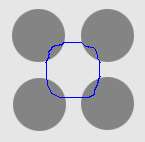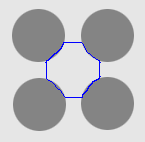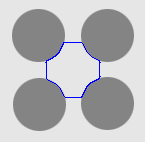 |
| Geodesic |  |  | 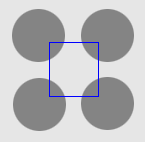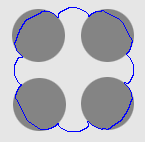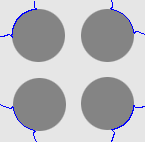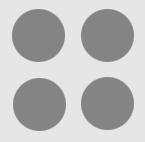 |
| GGVF |  | 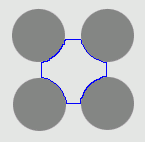 | 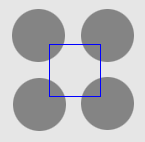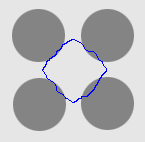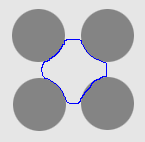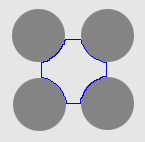 |
| GeoGGVF |  | 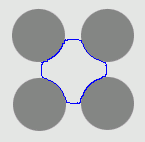 | 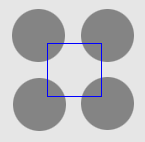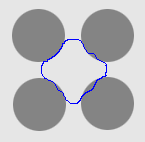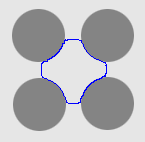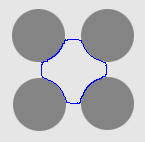 |
| CVF |  | 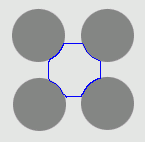 | 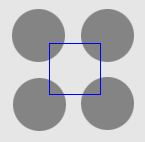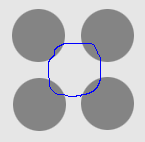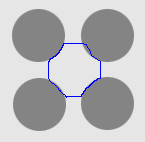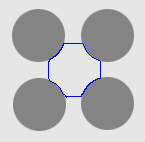 |
| MAC |  |  | 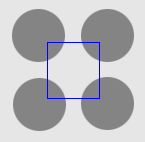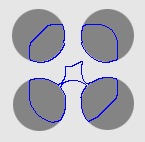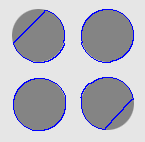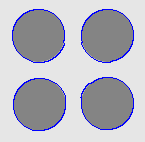 |
2. Recovering acute concavities
- Outside boundary initialisation
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF |  | 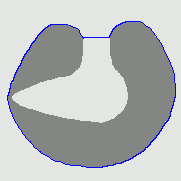 |  |
| Geodesic |  |  |  |
| GGVF |  | 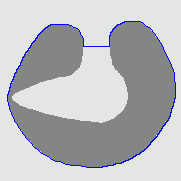 |  |
| GeoGGVF |  |  |  |
| CVF |  |  |  |
| MAC |  |  |  |
- Cross boundary initialisation
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF | 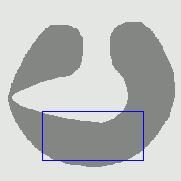 |  | 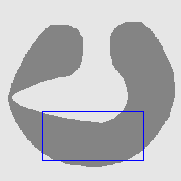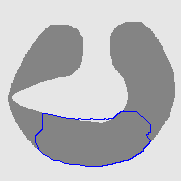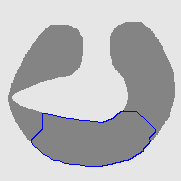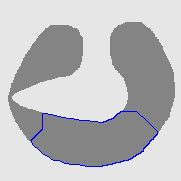 |
| Geodesic |  |  | 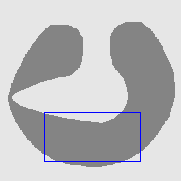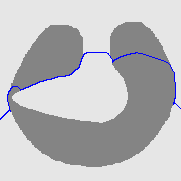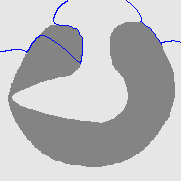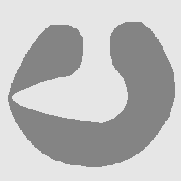 |
| GGVF |  |  | 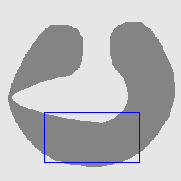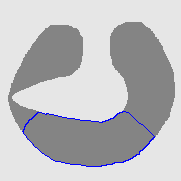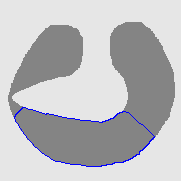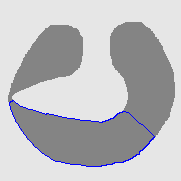 |
| GeoGGVF |  |  | 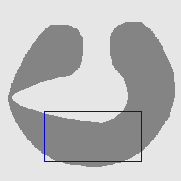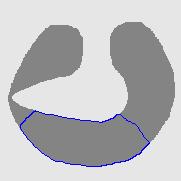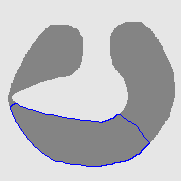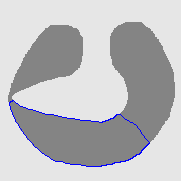 |
| CVF |  |  | 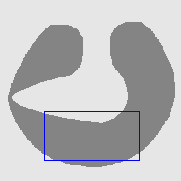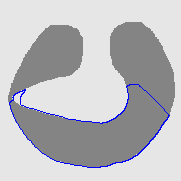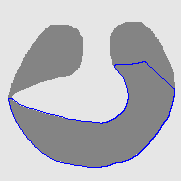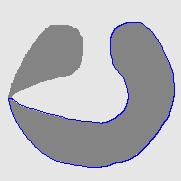 |
| MAC |  |  | 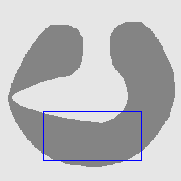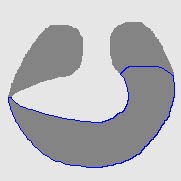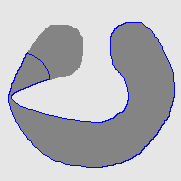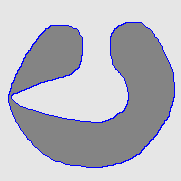 |
3. Handling complex geometries and topologies
- Recover a swirl shape
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF |  |  |  |
| Geodesic |  |  |  |
| GGVF |  |  |  |
| GeoGGVF |  |  |  |
| CVF |  |  |  |
| MAC |  |  |  |
- Recover text "PAMI"
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF |  |  |  |
| Geodesic |  |  |  |
| GGVF |  |  |  |
| GeoGGVF |  |  |  |
| CVF |  |  |  |
| MAC |  |  |  |
4. Recovery of broken boundaries and weak edges
- Broken boundary recovery
| Tip Initialisation | Cross-boundary Initialisation | |
| DVF |  | 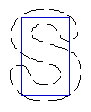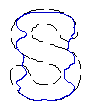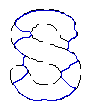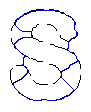 |
| Geodesic |  |  |
| GGVF |  | 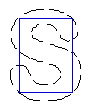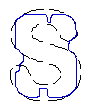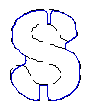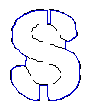 |
| GeoGGVF |  | 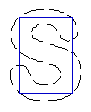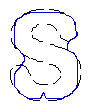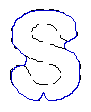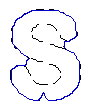 |
| CVF |  | 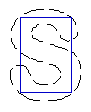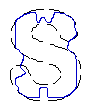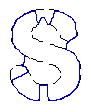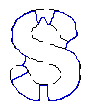 |
| MAC |  | 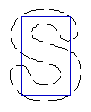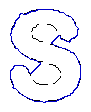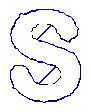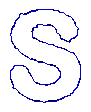 |
- Weak edge recovery
| Initial Snake | Stabilised Snake | Evolving Contours | |
| Geodesic |  |  |  |
| GGVF |  |  |  |
| CPM |  |  |  |
| MAC |  |  |  |
5. Arbitrary initialisations in MAC
| Initial Snake | Stabilised Snake | Evolving Contours |
 |  |  |
 |  |  |
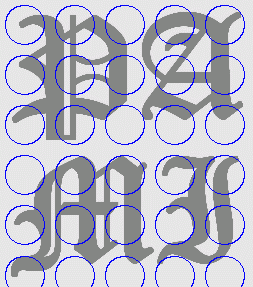 |  | 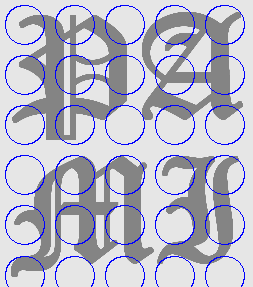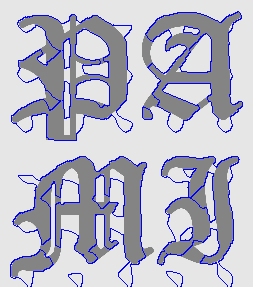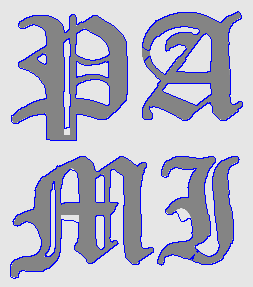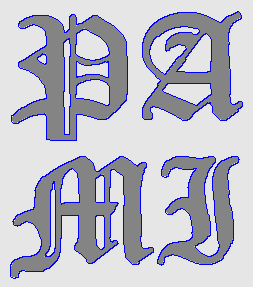 |
6. Noise sensitivity in MAC
| Initial Snake | Stabilised Snake | Evolving Contours | |
| 10% noise |  |  |  |
| 20% noise |  |  |  |
| 30% noise |  |  |  |
| 40% noise |  |  |  |
| 50% noise |  |  |  |
7. On real images
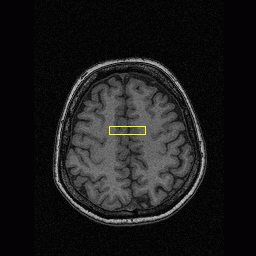
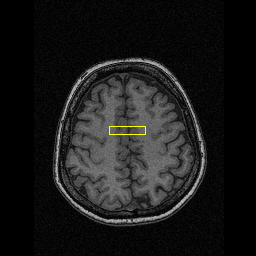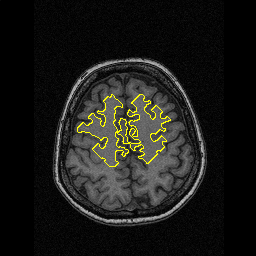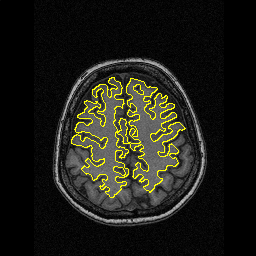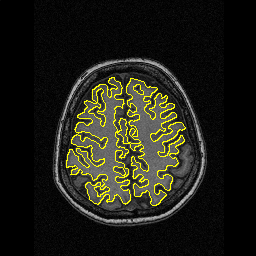
- Brain MRI image
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF | 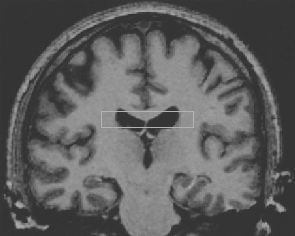 | 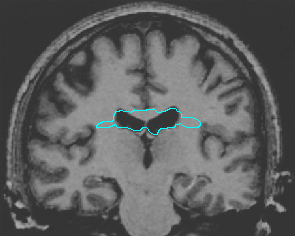 | 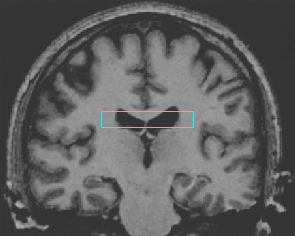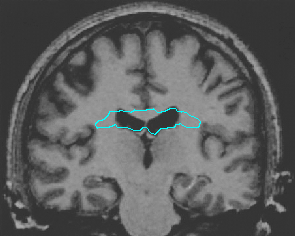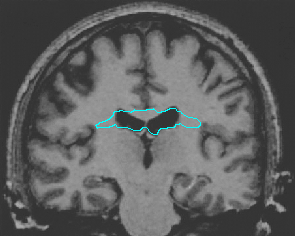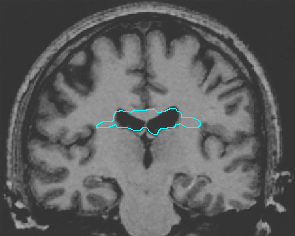 |
| Geodesic |  | 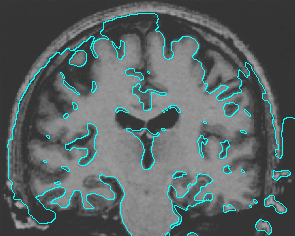 | 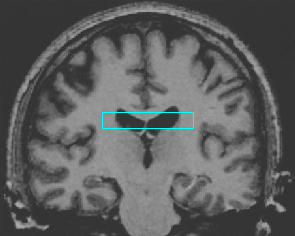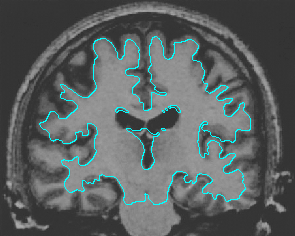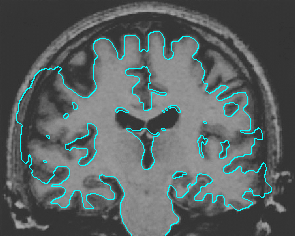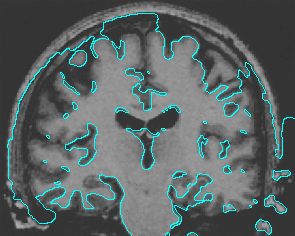 |
| GGVF |  | 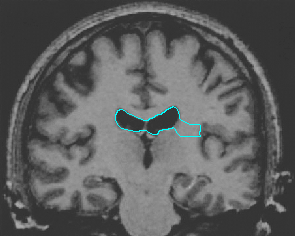 | 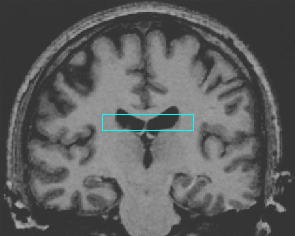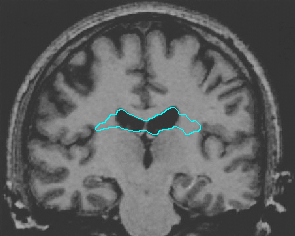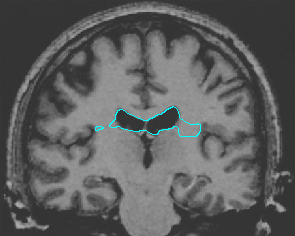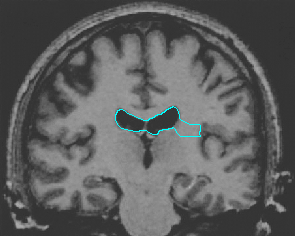 |
| GeoGGVF |  | 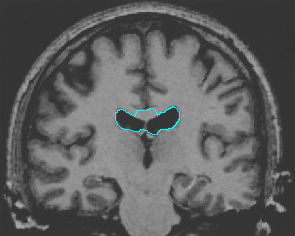 | 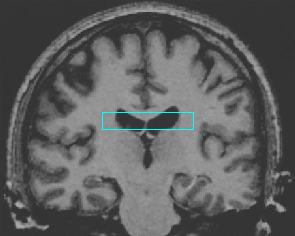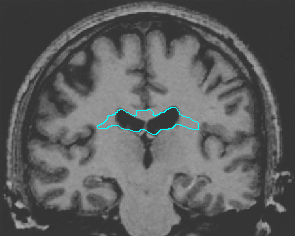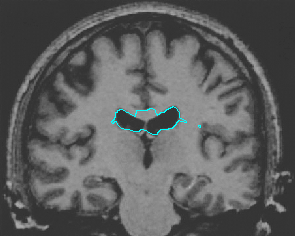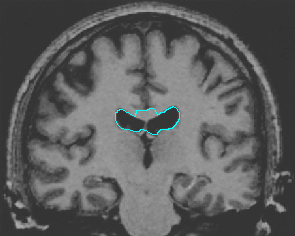 |
| CPM | 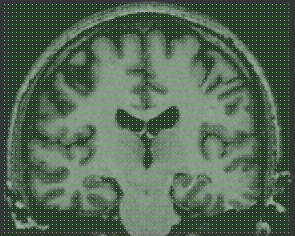 | 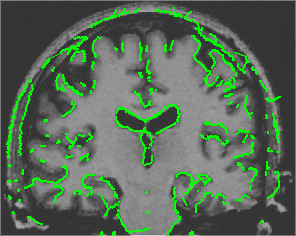 | 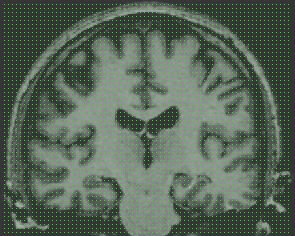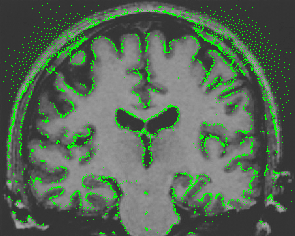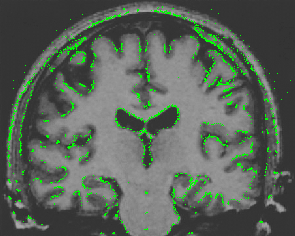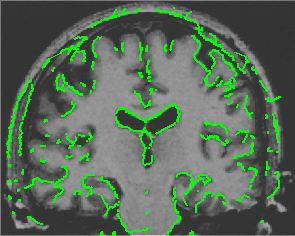 |
| MAC |  | 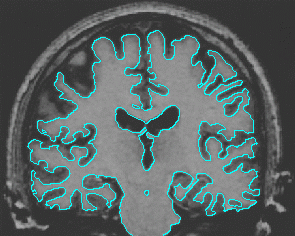 | 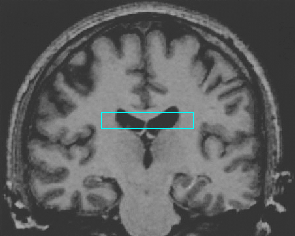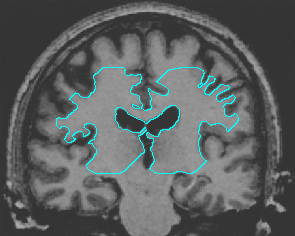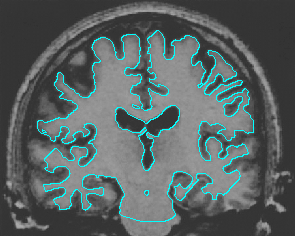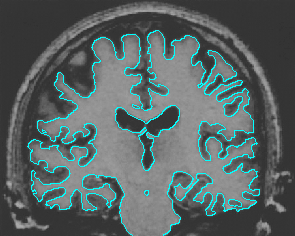 |
- Non-medical image
| Initial Snake | Stabilised Snake | Evolving Contours | |
| DVF |  | 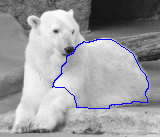 |  |
| Geodesic |  |  |  |
| GGVF |  |  |  |
| GeoGGVF |  |  |  |
| CPM |  |  |  |
| MAC |  |  |  |
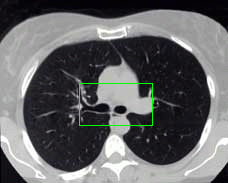
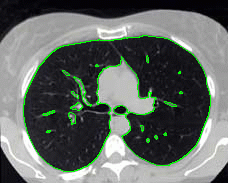
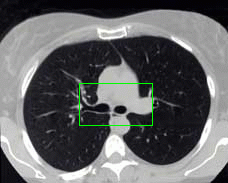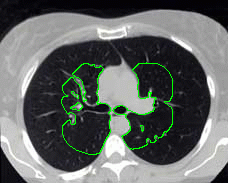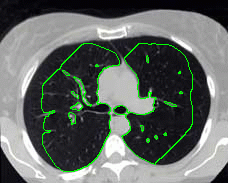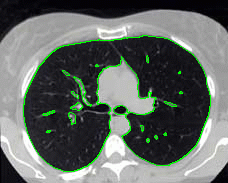
- More MAC results
| Initial MAC | Stabilised MAC | Evolving Contours |
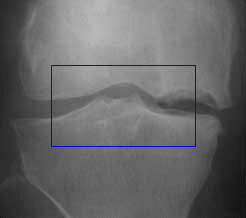 | 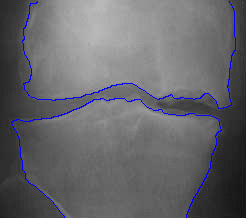 | 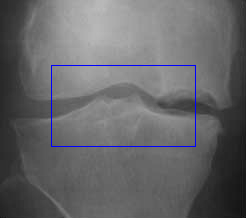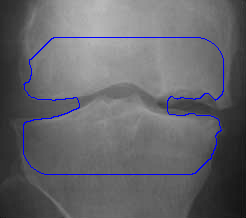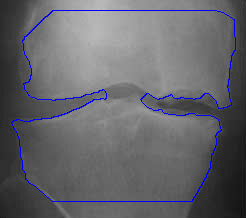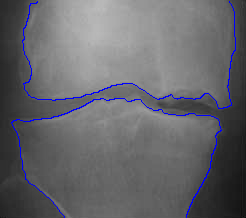 |
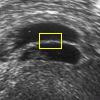 | 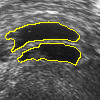 | 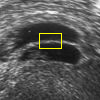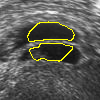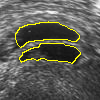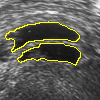 |
 |  |  |
 |  |  |
 | 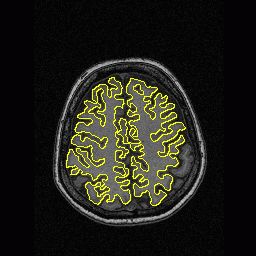 |  |
8. MAC with dual level sets
| Initial MAC/Shape | Stabilised MAC/Recovered Shape | Evolving Contours/Shapes | |
| Dual MAC | 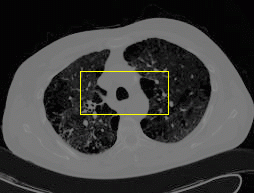 | 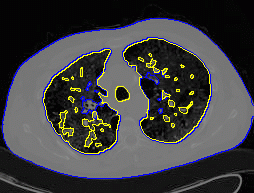 | 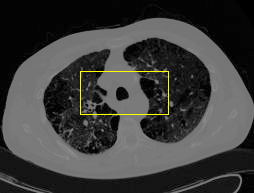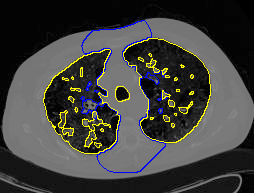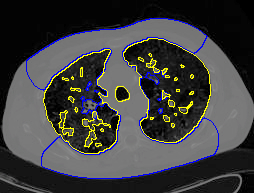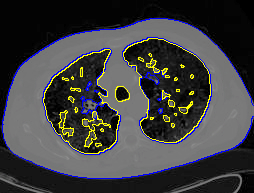 |
| Recovered shape with level set 1 |  | 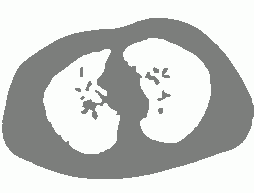 |  |
| Recovered shape with level set 2 |  | 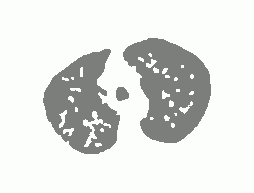 |  |
Software Downloading
An executable demo software written in JAVA for both Linux and Windows platforms can be downloaded from HERE. Please email me for password to unzip: x.xie at swansea.ac.uk
- Latest release: MAC-exe-release3.1.zip (June 2008).
Publications
- Xianghua Xie and Majid Mirmehdi, MAC: Magnetostatic Active Contour Model, IEEE Transactions on Pattern Analysis and Machine Intelligence (T-PAMI), volume 30, number 4, pages 632 - 646, IEEE CS Press, April 2008.
- Xianghua Xie and Majid Mirmehdi, Magnetostatic Field for the Active Contour Model: A Study in Convergence, In Proceedings of the 17th British Machine Vision Conference, pages 127-136, BMVA press, September 2006.
- Xianghua Xie, Si Yong Yeo, Majid Mirmehdi, Igor Sazonov, and Perumal Nithiarasu, Image Gradient Based Level Set Methods in 2D and 3D, In Deformation Models, Edited by G. Hidalgo et al., Springer, 2013.
