Geometric Potential Force For3-D Deformable Model
A novel 3-D deformable model based on a geometrically induced external force field is proposed, which can be conveniently generalized to arbitrary dimensions. The external force field is based on hypothesized interactions between the relative geometries of the deformable model and the object boundary characterized by image gradients. The evolution of the deformable model is solved using the level set method so that topological changes are handled automatically. The dynamic interaction forces between the geometries can greatly improve the deformable model performance in acquiring complex geometries and highly concave boundaries, and it gives the deformable model a high invariancy in initialization configurations. The bidirectionality of the external force field allows the new deformable model to handle arbitrary cross-boundary initializations, and facilitates the handling of weak edges and broken boundaries. In addition, the new deformable model can effectively overcome image noise, by enhancing the geometrical interaction field with a nonlocal edge-preserving algorithm.
Geometric Potential Force (GPF)
The external force field is called the geometric potential force (GPF) field as it is based on the hypothesized geometrically induced interactions between the relative geometries of the deforming surface and the object boundaries (characterized by image gradients).
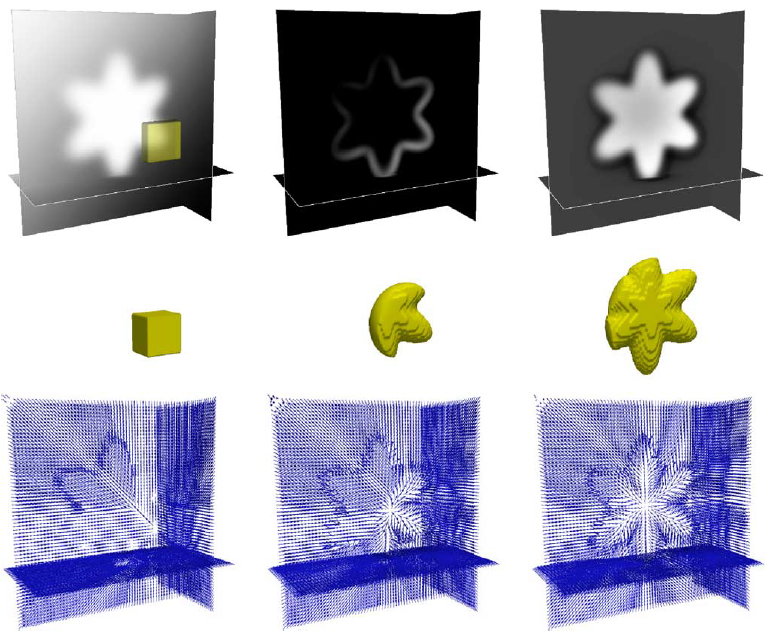 |
| GPF: (top) input image and initial deformable model, corresponding edge map, and computed geometric potential field; (middle) initial and evolving deformable models, and (bottom) associated GPF vector field. |
Example results - rings segmentation from noisy image
| EI model |  |
| Proposed GPF model |  |
Example results - shape recovery from synthetic images
| Isosurfaces of synthetic shapes |  |
| Initializations (yellow) |  |
| Geodesic |  |
| GGVF |  |
| Proposed GPF |  |
| Foreground (FG), background (BG) and overal segmentation accuracies of the above synthetic shapes using Geodesic, GGVF and the proposed GPF models. |
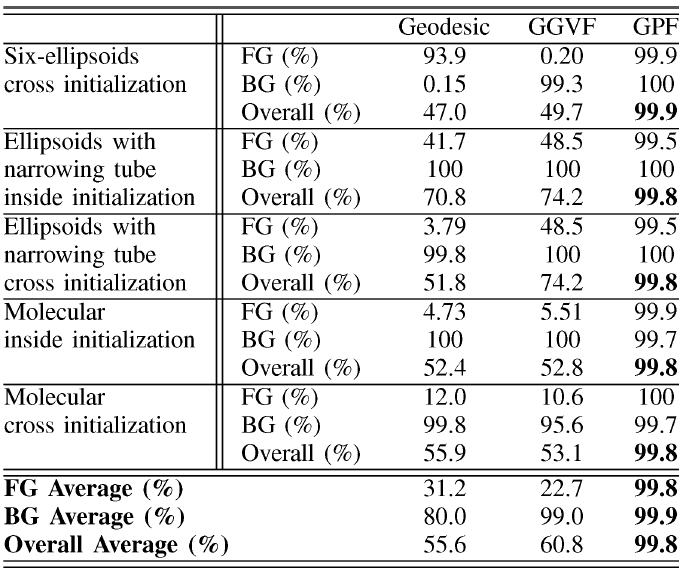 |
Example results - shape recovery from weak edges
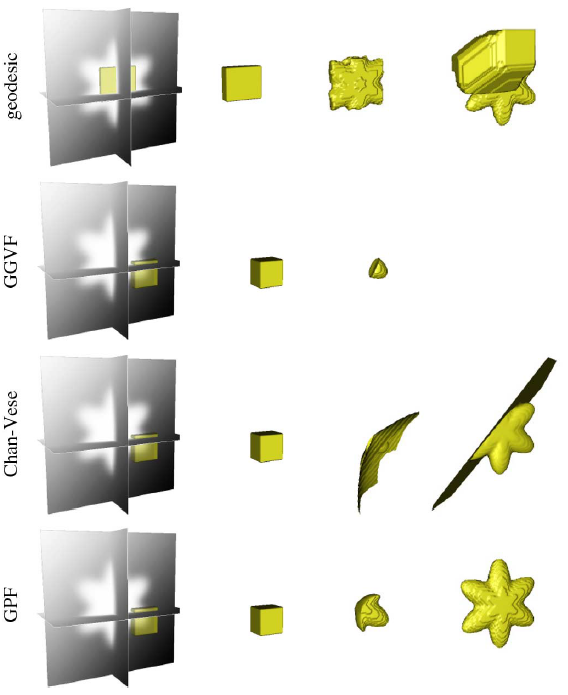 |
Example results - segmentation using GPF with arbitrary initialization
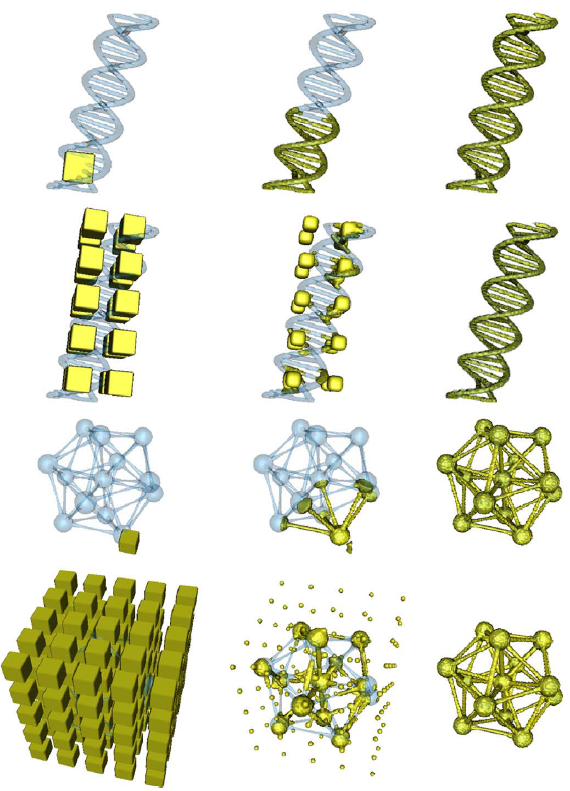 |
Example results - shape recovery from noisy image using GPF
 |
Example results - segmentation of human aorta CT image
| Geodesic |  |
| GGVF |  |
| proposed GPF | 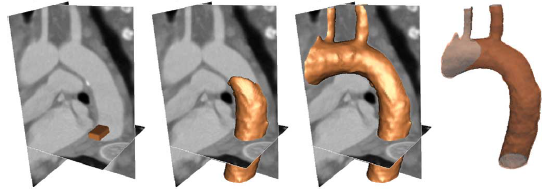 |
Example results - segmentation of cerebral artery MRI image
| Geodesic |  |
| GGVF |  |
| Chan-Vese |  |
| proposed GPF |  |
Example results - segmentation of femur CT image
| Geodesic | 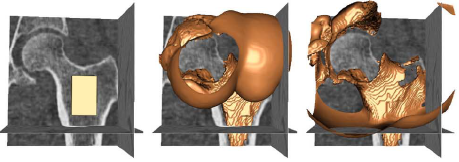 |
| GGVF | 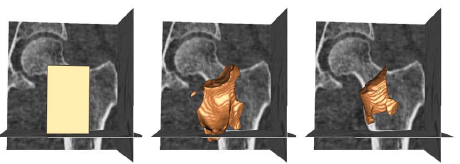 |
| Chan-Vese | 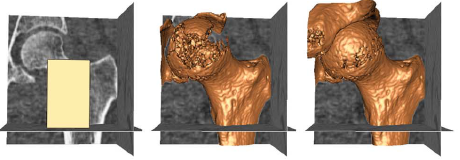 |
| EI | 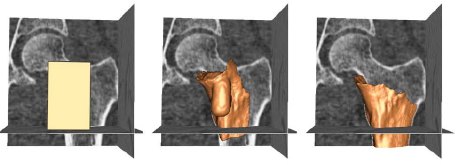 |
| proposed GPF | 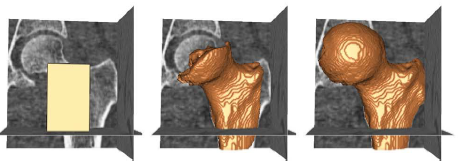 |
Example results - segmentation of multi-branch carotid artery CT image using GPF
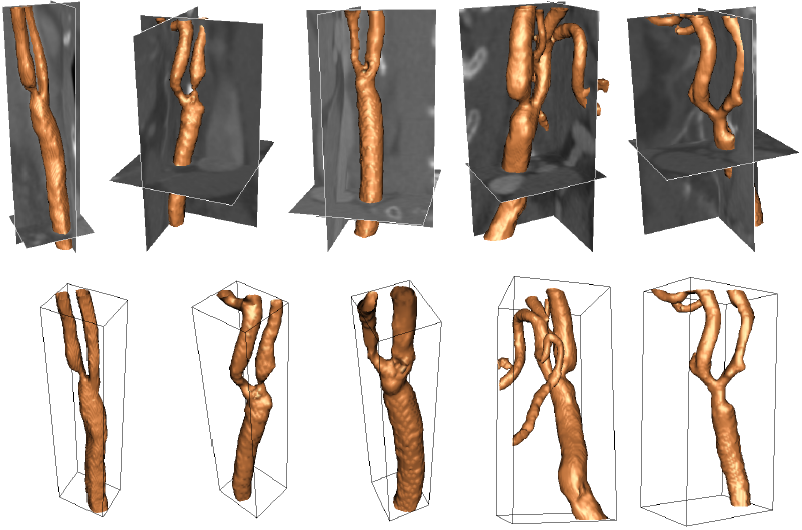 |
Publications
- S. Yeo, X. Xie, I. Sazonov and P. Nithiarasu, Geometrically Induced Force Interaction for Three-Dimensional Deformable Models, IEEE Transactions on Image Processing (T-IP), volume 20, number 5, pages 1373 - 1387, IEEE CS Press, May 2011.
- S. Y. Yeo, X. Xie, I. Sazonov, P. Nithiarasu, GPF Deformable Model based Vessel Segmentation in CT, In Proceedings of the 16th Conference on Medical Image Understanding and Analysis, July 2012.
- S. Yeo, X. Xie, I. Sazonov, P. Nithiarasu, Segmentation of Vessel Geometries from Medical Images using GPF Deformable Model, In Proceedings of the International Conference on Pattern Recognition Applications and Methods, February 2012.
- Si Yong Yeo, Xianghua Xie, Igor Sazonov and Perumal Nithiarasu, Geometric Potential Force for the Deformable Model, In Proceedings of the 20th British Machine Vision Conference, BMVA press, September 2009.
- Xianghua Xie, Si Yong Yeo, Majid Mirmehdi, Igor Sazonov, and Perumal Nithiarasu, Image Gradient Based Level Set Methods in 2D and 3D, In Deformation Models, Edited by G. Hidalgo et al., Springer, 2013.
