Deformable Segmentation With Arbitrary Initializations
We propose a unified approach to deformable model-based segmentation. The fundamental force field of the proposed method is based on computing the divergence of a gradient convolution field (GCF). Then, using this proposed external force field, we derive a more salient representation for contour evolution that does not only lead to global minimum through convex relaxation but also can achieve the same result using the conventional gradient descent with an intrinsic regularization. Moreover, nonlinear diffusion can be conveniently applied to GCF to improve its performance in dealing with noise interference. Additionally, the derived deformable model can work well in 3D or higher dimensions because GCF can be naturally extended to higher dimensions.
Proposed Solution Scheme
External force
We derive the gradient convolution field (GCF) by convolving the image gradient field with an inverse distance kernel function and propose to use the GCF and its divergence as an image feature, which can be considered as a region indicator and has explicit relationship to the MAC model.
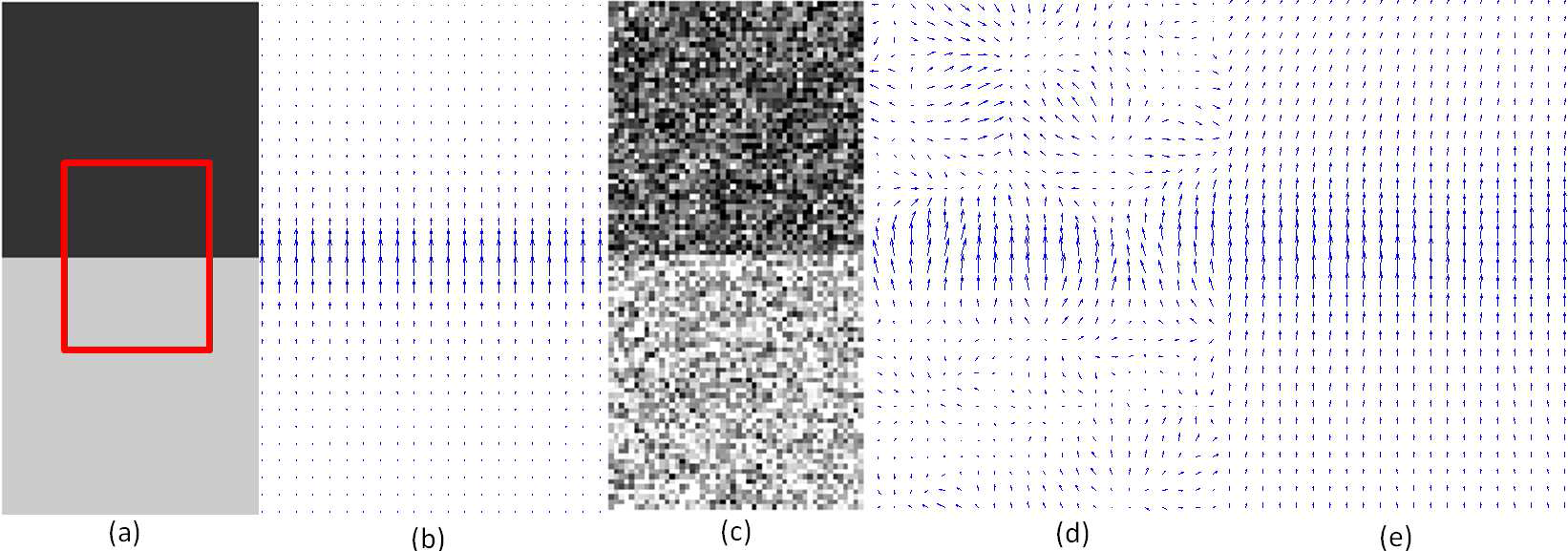 |
| Fig. 1 (a) an ideal image, (b) GCF of the clear image, (c) the noise corrupted version (d) GCF of the noisy image, (e) diffused GCF using the proposed method. The vector fields are zoomed in at the location highlighted in (a) for clear visualization. |
Deformable model
A deformable model is derived using the divergence of GCF as its external force.
Diffusion scheme
A tensor diffusion scheme is proposed to diffuse the GCF in order to improve the performance of the deformable model, where the edges are better preserved and image noise can be more efficiently removed even though they may appear far from strong edges.
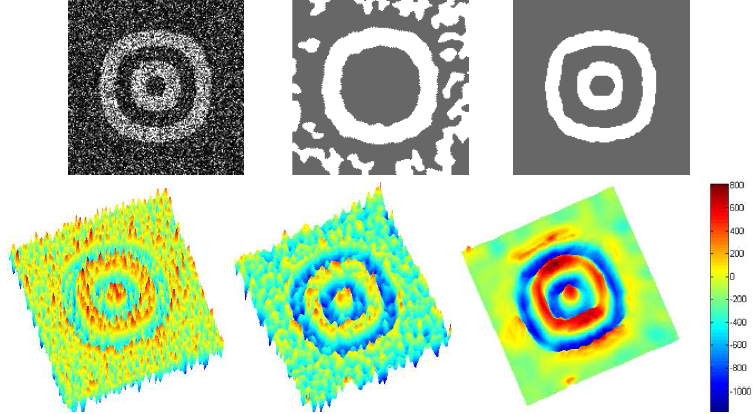 |
| Fig. 2: First row from left: an noisy image, result obtained using Laplacian diffusion, result based on the proposed method. Second row from left: the initial force field, diffused force field using Laplacian diffusion, and finally the diffused result using the proposed method. |
Level set implementation with a regularized scheme
An intrinsic level set regularization scheme is used for performing its numerical implementation in 2D, which is originally motivated from smoothing the transition between different level sets. The proposed method can achieve initialization invariance in practice by using this intrinsic level set regularization.
 |
| Fig. 3: Results using the proposed method for weak boundaries. Row 1 shows various initializations and Row 2 presents the converged results. |
Global minimizer with convex relaxation
The global minimizer of the proposed deformable model is achieved by applying convex relaxation to formulate the energy functional, where the level set implementation can be readily extended from 2D to 3D with small computational overhead.
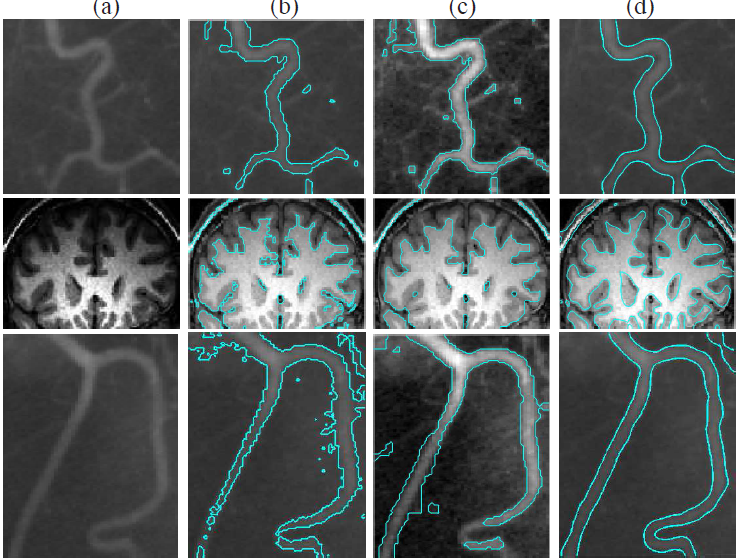 |
| Fig. 4: Results without initialization. (a) original image, (b) SBCV, (c) GCCV and (d) the proposed method. |
Active surfaces using GCF
The 2D evolving curves can be naturally generalized to higher dimensional spaces, e.g. active surfaces in 3D.
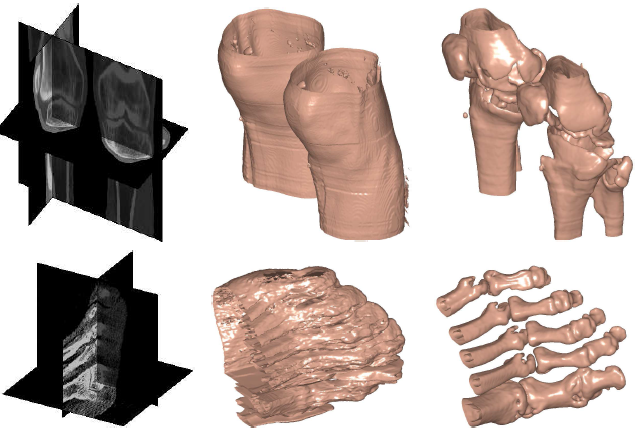 |
| Fig. 5: Results using SBCV (Column 2), and the proposed method (Final column) in the biomedical datasets of the Knee (379 × 229 × 305), Foot (256 × 256 × 256), Lobster (301 × 324 × 56) and Tooth (92 × 78 × 161). Column 1 shows the 3-D view of example slices. |
Reference
- H. Zhang and X. Xie. Divergence of Gradient Convolution: Deformable Segmentation with arbitrary initializations. IEEE Trans. Image Processing, Vol.24, No. 11, 3902-3914, November 2015.
